通过主方程推广熵公式

熵是物理学中最重要和最广泛研究的物理量之一，几个世纪以来，它的值一直被用简单的数学关系稳健地描述。然而，匈牙利科学院(Hungarian Academy of Science)的Tamás Biró认为，不管这个公式多么优雅，它隐藏着一系列更为复杂的关系。通过构建描述这些关系的“主方程”，Biró和他的同事们正在利用统计学研究各种各样的问题，如强子的形成、生物多样性的变化和Facebook上受欢迎的模式。

我们周围的每个系统都有不同程度的混乱与之相关。金属内部的原子排列整齐，高度有序，而空气中气体分子的运动则要混乱得多，难以预测。自19世纪以来，物理学家用一个叫做“熵”的量来描述这种混沌。在物理过程中发生的熵的变化形成了最基本的物理定律之一的基础:热力学第二定律。该定律指出，在任何与外界封闭的系统中，熵不应随时间而减少;因此，宇宙作为一个整体变得更加混乱。

正如Biró博士所描述的，这种不可避免的熵的增加代表了粒子剩余排列的数量的减少，或“状态”，系统可以发现自己在单向的时间推移中。“从宏观上讲，熵从未被证明是自发减少的;这与‘时间之箭’或不可逆有关，”他解释道。“自然界中的许多过程只会在某些特定的状态中结束，而它们可能会在大量可能状态中的任何一种中开始。在一个复杂的封闭系统中，所有的微观变化都以一种总熵永远不会减少的方式共同作用。”

为了量化熵，物理学家最终需要使用统计学来研究粒子是如何随着时间的推移以不同的方式运动的。Biró博士继续说:“动力学理论和它的追随者，统计物理学，依赖于我们对熵的知识。”“它们可以被视为基于处于特定状态的概率的给定数学公式。所有随机或‘随机’模型现在都被检查是否满足这样一个定理，在它们的计算中考虑了随机力。”即使经过几个世纪的仔细研究，这些数学描述也一次又一次被证明能够有力地描述真实的物理系统。然而，在他们的研究中，Biró博士和他的同事们现在想让这个理论更进一步。

总结玻尔兹曼公式
在19世纪70年代，奥地利物理学家路德维希·玻尔兹曼(Ludwig Boltzmann)能够将熵的数量减少到一个非常简单、优雅的公式。他提出，它的值与系统在当前条件下可能存在的状态数有对数关系。然而，尽管这个公式在数学上预测熵的变化非常有效，Biró博士和他的同事们认为它不能完全解释构成它的更复杂的物理过程。在他们的研究中，研究人员旨在推广玻尔兹曼的简单方程;确定建立整体对数关系的数学关系。

在一个复杂的封闭系统中，所有的微观变化都以一种总熵永远不会减少的方式共同作用。

Biró博士说:“我们的研究与推广玻尔兹曼原始公式的新努力相结合，该公式包含对数——一个将乘积映射为和的简洁函数。”"有什么更普遍的动力学过程使玻尔兹曼对数不可避免"通过几项研究，研究人员已经使用真实世界的熵变化的例子来研究玻尔兹曼对数是如何以这种方式推广的。到目前为止，他们分析的问题范围从粒子物理学的基本问题到社交媒体上的互动模式。

解决强子化问题
在宇宙动力学的最初时刻，夸克和胶子等基本粒子作为自由流动的气体汤或等离子体元素存在。然而，这些粒子最终无法独自存在;在大爆炸后的十万分之一秒内，它们聚集在一起形成了稳定的结构，称为强子——由胶子结合在一起的三个夸克组成。然而，“强子化”的过程给物理学家提出了一个问题:既然强子似乎比夸克-胶子等离子体有序得多，宇宙的总熵怎么可能增加呢?

在他们的研究中，Biró博士和同事们基于巴西物理学家Constantino Tsallis的早期工作，提出了一种看待这个问题的新方法。在20世纪80年代，Tsallis起草了一套新的统计参数来推广玻尔兹曼的公式，为熵的特殊情况产生了一个新的统计分支。特别是，他的方程产生了一系列新的概率分布——描述系统中单个粒子处于某个位置的概率的统计公式。由Tsallis推导的概率分布可以比以前的模型更真实地描述物理系统的熵。

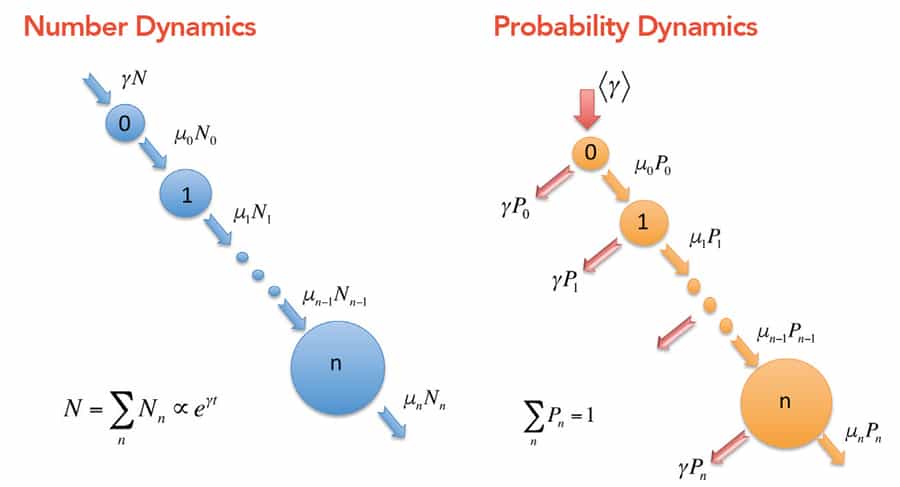
基于Tsallis的工作，Biró博士的团队可以构建一套“主方程”——建立玻尔兹曼公式的数学关系，但更好地描述单个物理系统的行为。

这使得研究人员可以从一个新的角度来研究强子化问题;这为我们提供了新的见解，让我们了解在宇宙的最初时刻，熵是如何整体增加的。Biró博士和他的同事们也将他们的数学应用于其他情况;测试他们模型的有效性的系统包括社交媒体上的流行模式，收入和财富的分配，以及定居点和生态系统的规模分布。

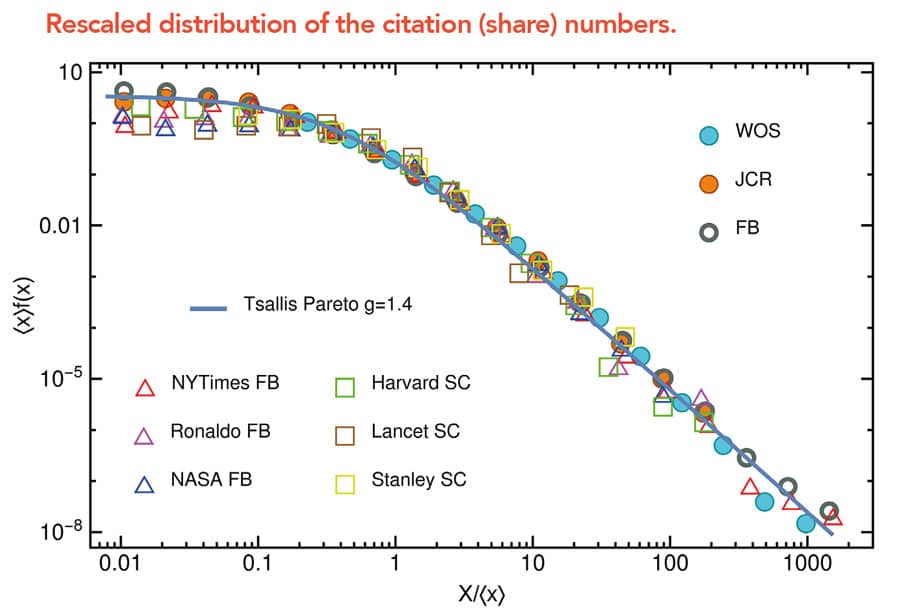
一组主方程
通过这些研究，Biró博士和他的同事们已经在推广玻尔兹曼的原始公式方面取得了长足的进步，他们使用了根据统计物理原理改编的数学方法，而统计物理原理正是萨里斯首次在熵的例子中推广的。正如Biró博士解释的那样，“我们发现非线性主方程:动力学方程处理系统处于给定状态的概率，而不是线性的，而是通过一些更复杂的函数，导致对熵使用非对数公式。”利用这种复杂的数学，研究人员可以构建熵概率分布，更密切地反映那些可以在自然界中观察到的分布。

最终，这些主方程使得Biró博士和他的同事能够模拟系统的概率分布是如何随着时间的推移和熵的增加而演化的。随着时间的推移，熵的增加将意味着与系统相关的概率分布有望发生变化。Biró博士继续说:“我们展示这一点的方法依赖于‘熵散度’:两个概率分布之间的非对称距离公式。”“稳定的非线性主方程模型描述了概率的变化，总是趋向于一个不再变化的、平稳的分布。”因此，该团队的主方程可以模拟真实系统的熵随时间的变化。

Biró博士和他的同事在推广玻尔兹曼的原始公式方面取得了长足的进步。

通过这项工作，Biró博士和他的同事可以构建一个“非广泛的”熵公式，它解释了在一个过程结束后，系统的概率分布如何独立于大多数材料的初始概率分布。由于熵距离关系更能反映现实，主方程可以用来构建一个高度广义的计算熵的公式。Biró博士解释说:“许多物理系统都是由随机主方程描述的。”“它们对应的平稳分布属于最大熵;因此，熵也可以定义为从均匀分布出发的熵散度。

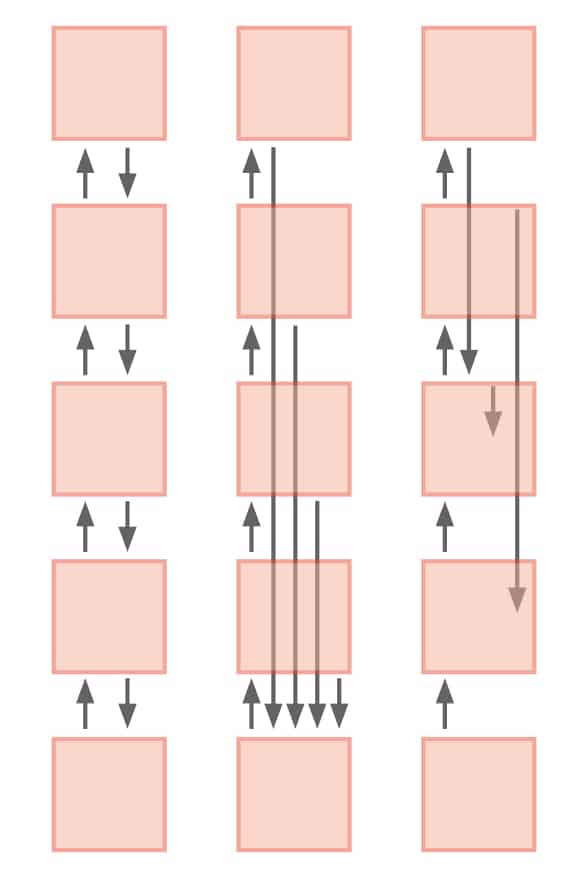
应用模型
Biró博士及其同事所描述的数学已经可以用来模拟熵的变化，这些变化在各种不同的系统中呈现出来。Biró博士总结道:“我们将我们的数学模型应用于各种物理系统，包括受欢迎程度的复杂网络，如引文或Facebook上的点赞，城市规模分布，大型对撞机实验中产生的强子能量，大学之间的学生交流网络，等等。”然而，该团队的数学描述仍远未完成。在未来的工作中，研究人员将研究更复杂的非线性主方程;使我们对熵的工作原理有了更深入的了解。